Pengertian Uji T dan Uji F serta Cara Analisis dengan SPSS
Pengertian Uji T dan Uji F pada Regresi Linear Berganda serta Cara Analisis dengan SPSS
Pada artikel ini kita akan mempelajari cara uji t dan uji f pada regresi linear berganda dengan SPSS, serta cara interpretasi output uji t dan uji f.
Kita mulai dari pengertian uji t
Pengertian Uji T
Uji t adalah uji yang digunakan untuk mengetahui ada tidaknya pengaruh secara parsial variabel independent (variabel X) terhadap variabel dependent (variabel Y). Maksud pengaruh parsial yaitu pengaruh sendiri-sendiri oleh variabel independent. Pada kasus uji regresi linear berganda dengan dua variabel independent, berarti kita akan melihat pengaruh variabel independent pertama (X1) terhadap variabel dependent (Y) dan melihat pengaruh variabel independent kedua (X2) terhadap variabel dependent (Y).
Pada paragraf sebelumnya Saya menyebutkan regresi linear berganda. Apa itu uji regresi linear berganda? Uji regresi linear berganda merupakan uji yang digunakan untuk mengetahui ada tidaknya pengaruh dari dua atau lebih variabel independent terhadap variabel dependent (Y).
Apabila hanya terdapat satu variabel independent yang mempengaruhi variabel dependent, maka disebut analisis regresi linear sederhana. Jadi untuk uji regresi berganda, variabel independentnya minimal terdapat dua variabel.
Langkah-langkah uji t
1. Menentukan hipotesis
Sebagai contoh regresi linear dengan dua variabel independent
H0 = Variabel X1, X2 secara parsial tidak berpengaruh secara signifikan terhadap variabel Y.
H1 = Variabel X1, X2 secara parsial berpengaruh secara signifikan terhadap variabel Y.
2. Menentukan derajat kepercayaan 95% (α= 0,05)
3. Menentukan pedoman pengambilan keputusan
Terdapat dua cara dalam pengambilan keputusan uji f, yaitu menggunakan nilai signifikansi dan menggunakan t tabel.
Menggunakan signifikansi:
Apabila nilai sig (signifikansi) > 0,05 maka H0 diterima
Apabila nilai sig (signifikansi) < 0,05 maka H0 ditolak
Menggunakan t tabel
Apabila nilai t hitung < t tabel maka H0 diterima
Apabila nilai t hitung > t tabel maka H0 ditolak
4. Membuat kesimpulan.
Pengertian Uji F
Uji f adalah uji yang digunakan untuk mengetahui ada tidaknya pengaruh secara simultan variabel independent (X) terhadap variabel dependent (Y). Maksud pengaruh simultan yaitu pengaruh bersama-sama beberapa variabel independent terhadap variabel dependent. Apabila terdapat tiga variabel independent (X1, X2, X3), maka kita akan melihat apakah variabel X1, variabel X2, dan variabel X3 berpengaruh secara bersama-sama terhadap variabel dependent (Y).
Langkah-langkah uji f
1. Menentukan hipotesis
Sebagai contoh, kasus regresi linear dengan dua variabel independent:
H0 = Variabel X1, X2 secara simultan tidak berpengaruh secara signifikan terhadap variabel Y.
H1 = Variabel X1, X2 secara simultan berpengaruh secara signifikan terhadap variabel Y.
2. Menentukan derajat kepercayaan 95% (α= 0,05)
3. Menentukan pedoman pengambilan keputusan
Terdapat dua cara dalam pengambilan keputusan uji f, yaitu menggunakan nilai signifikansi dan menggunakan f tabel.
Menggunakan signifikansi:
Apabila nilai sig (signifikansi) > 0,05 maka H0 diterima
Apabila nilai sig (signifikansi) < 0,05 maka H0 ditolak
Menggunakan f tabel
Apabila nilai f hitung < f tabel maka H0 diterima
Apabila nilai f hitung > f tabel maka H0 ditolak
4. Membuat kesimpulan
Contoh Kasus Uji T dan Uji F Pada Regresi Linear Berganda
Seorang Supervisor pemasaran suatu perusahaan ingin melakukan peramalan atas besarnya jumlah penjualan berdasarkan jumlah sales dan harga produk. Terdapat tiga variabel penelitian. Jumlah sales dan harga produk merupakan variabel independent dan penjualan merupakan variabel dependent. Berikut ini datanya:
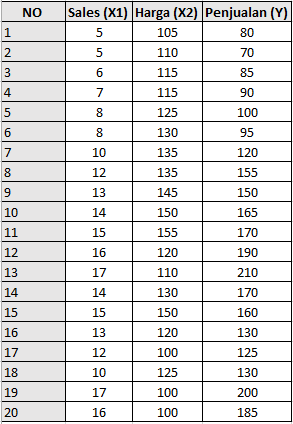 |
| Data Kasus Uji t dan Uji f pada Regresi Linear Berganda |
Data tersebut akan kita analisis uji t dan uji f menggunakan software SPSS.
Langkah-langkah uji t dan uji f dengan SPSS
1. Buka software SPSS, langkah awal yaitu input data di SPSS. Klik tampilan variable view untuk membuat variabel.
Membuat variabel X1(variabel sales):
Ketik X1 di kolom Name, kolom Decimals diubah menjadi 0, pada bagian Label ketik “jumlah sales”, pada kolom Measure pilih scale.
Membuat variabel X2 (variabel harga produk)
Ketik X2 di kolom Name (baris kedua), kolom Decimals diubah menjadi 0, pada bagian label ketik “harga produk-ribu”, pada kolom Measure pilih scale.
Membuat variabel Y (variabel penjualan)
Ketik Y di kolom Name (baris ketiga), kolom Decimals diubah menjadi 0, pada bagian label ketik “penjualan-juta”, pada kolom Measure pilih scale.
Setelah selesai membuat variabel, maka tampilan variabel view akan seperti ini
 |
| Tampilan Variable View SPSS |
Baca Juga: Cara Input Data di SPSS
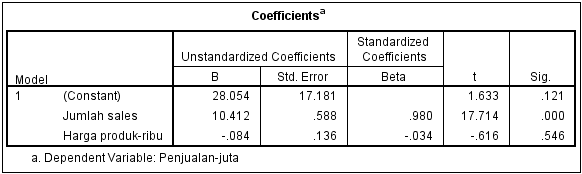
2. Selanjutnya klik tampilan data view, lalu copy data dari file excel, lalu paste kan ke dalam SPSS. Sehingga tampilan Data View akan seperti berikut:
 |
| Tampilan Data View SPSS |
3. Setelah melakukan input data di SPSS. Selanjutnya melakukan analisis uji t dan uji f regresi linear berganda dengan klik Analyze, pilih Regression, lalu pilih Linear pada menu, sehingga muncul kotak dialog Linear Regression.
4. Masukkan variabel jumlah sales (X1) dan harga (X2) pada kotak Independent(s) dan variabel penjualan (Y) ke kotak Dependent.
5. Selanjutnya klik OK, sehingga SPSS menampilkan hasil sebagai berikut:
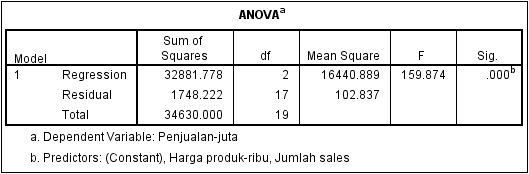 |
| Output ANOVA |
 |
| Output Coefficients |
Terdapat beberapa tabel yang muncul, Cuma untuk analisis uji t dan uji f Kita menggunakan dua tabel diatas.
Membaca Output uji t dan uji f
Analisis Uji F atau uji Simultan
ANOVA atau disebut juga analisis varian, yaitu uji koefisien regresi yang digunakan untuk mengetahui ada tidaknya pengaruh secara bersama-sama beberapa variabel independent (X) terhadap variabel variabel dependent (Y).
Output ANOVA atau disebut juga uji F, merupakan tabel yang akan digunakan untuk menjawab hipotesis regresi linear berganda.
Dibawah ini rumusan hipotesis regresi berganda untuk permasalahan diatas:
H1 = Variabel X1 (jumlah sales) dan X2 (harga) secara bersama-sama berpengaruh secara signifikan terhadap variabel Y (penjualan).
Setelah tahu rumusan hipotesisnya, Anda harus tahu pedoman pengambilan keputusan uji f. Berikut ini pedoman pengambilan keputusan uji f pada regresi berganda:
Jika nilai signifikansi (Sig.) < 0,05 maka H0 ditolak
Atau
Jika nilai f hitung > f tabel maka H0 ditolak
Pada tabel ANOVA diperoleh nilai Sig. (0,000) < 0,05 maka Ho ditolak. Karena H0 ditolak maka H1 diterima, jadi Variabel X1 (jumlah sales) dan X2 (harga) secara bersama-sama berpengaruh signifikan terhadap variabel Y (penjualan).
Disamping menggunakan nilai Sig (signifikansi), Anda juga dapat membandingkan nilai f hitung dengan nilai f tabel.
Diperoleh nilai f hitung 159.874 > f tabel (2;17;0,05) 3,59 maka H0 ditolak, Karena H0 ditolak maka H1 diterima, jadi Variabel X1 (jumlah sales) dan X2 (harga) secara bersama-sama berpengaruh signifikan terhadap variabel Y (penjualan).
Catatan:
Dalam mencari nilai F tabel menggunakan rumus = (jumlah variabel -1; n-k-1; α). n merupakan jumlah sampel, k adalah jumlah variabel independent, dan α merupakan tingkat signifikansi 0,05.
Analisis Uji t
Uji t (uji koefisien regresi secara parsial) digunakan untuk mengetahui apakah secara parsial variabel jumlah sales dan harga berpengaruh secara signifikan atau tidak terhadap variabel penjualan. Karena terdapat dua variabel independent, maka untuk analisisnya satu variabel satu variabel.
Pengujian koefisien variabel jumlah sales (b1)
Rumusan hipotesis untuk variabel jumlah sales:
H1 = variabel jumlah sales secara parsial berpengaruh terhadap penjualan.
Berikut ini pedoman pengambilan keputusan uji t:
Apabila diperoleh nilai Sig < 0,05 maka H0 ditolak
Atau
Apabila diperoleh nilai t hitung > t tabel maka H0 ditolak
Pada tabel Coefficients di baris jumlah sales diperolah nilai Sig sebesar 0,000 < 0,05 maka H0 ditolak. Karena H0 ditolak maka H1 diterima, jadi jumlah sales secara parsial berpengaruh terhadap penjualan.
Selain menggunakan nilai Signifikansi, Anda dapat membandingkan nilai t hitung dengan nilai t tabel.
Pada tabel Coefficients di baris jumlah sales diperolah nilai t hitung sebesar 17,714 > t tabel (17;0,025) 2,110 maka H0 ditolak. Karena H0 ditolak maka H1 diterima, jadi jumlah sales secara parsial berpengaruh terhadap penjualan.
Catatan:
Rumus untuk mencari t tabel yaitu : (n-k-1; α/2)
Dengan n merupakan jumlah sampel; k adalah jumlah variabel independent; α adalah 0,05 sehingga α/2 = 0,025.
Anda dapat membaca secara detail terkait cara membuat dan membaca t tabel melalui link ini.
Pengujian koefisien variabel harga (b2)
Berikut ini rumusan hipotesis untuk variabel harga:
H1 = variabel harga secara parsial berpengaruh terhadap penjualan.
Berikut ini pedoman pengambilan keputusan uji t:
Jika diperoleh nilai Sig < 0,05 maka H0 ditolak
Atau
Apabila diperoleh nilai t hitung > t tabel maka H0 ditolak
Pada tabel Coefficients pada baris variabel harga diperolah nilai Sig 0,546 > 0,05 maka H0 diterima, sehingga dapat disimpulkan harga secara parsial tidak berpengaruh terhadap penjualan.
Selain menggunakan nilai Signifikansi, Anda dapat membandingkan nilai t hitung dengan nilai t tabel.
Pada tabel Coefficients di baris harga produk diperolah nilai t hitung sebesar 0,616 < t tabel (17;0,025) 2,110 maka H0 diterima, jadi harga secara parsial tidak berpengaruh terhadap penjualan. Atau dengan kata lain, tidak terdapat hubungan yang signifikan antara variabel harga produk dengan variabel penjualan.
Catatan:
Pada t hitung kita menggunakan nilai mutlak, jadi tidak ada tanda negatif. Pada variabel harga diperoleh t hitung -0,616, maka nilai yang digunakan adalah 0,616.
Demikian artikel yang berjudul Pengertian Uji T dan Uji F serta Cara Analisis dengan SPSS. Terima kasih sudah membaca sampai sini.
Referensi:
Trihendradi, C., 2013. Step by Step IBM SPSS 21: Analisis Data Statistik. Yogyakarta: Penerbit Andi.
Purnomo, R. A. 2016. Analisis Statistik Ekonomi dan Bisnis dengan SPSS. Ponorogo: Penerbit Wade Group.



.png)

Komentar
Posting Komentar