Travelling Salesman Problem Menggunakan Algoritma Genetika

Pengertian Algoritma Genetika

Algoritma Genetika atau Genetic algorithm adalah algoritma optimasi yang terinspirasi oleh prinsip genetika dan seleksi alam, sebagaimana pada Teori Evolusi Darwin yang berjudul “Theory of Natural Selection”. 

Pada Teori tersebut dijelaskan bahwa individu-individu yang mempunyai kualitas yang bagus akan mempunyai peluang besar untuk bertahan hidup dan bereproduksi sehingga mewariskan karakteristiknya kepada keturunan-keturunannya. Sedangkan individu-individu yang mempunyai kualitas kurang bagus, maka akan tersingkir dari populasi secara perlahan (Hendrawan, 2007).

Baca juga: Algoritma Particle Swarm Optimization

Pengertian Travelling Salesman Problem (TSP)

Travelling Salesman Problem atau yang disingkat TSP merupakan permasalahan pengaturan rute dari suatu depot menuju ke semua titik layanan tanpa adanya pengulangan dan kembali ke titik awal (depot) dengan tujuan meminimalkan total jarak tertempuh. Berikut ini ciri-ciri permasalahan TSP yaitu: 

1. Perjalanan berawal dari depot dan akan kembali ke depot.
2. Ada sejumlah kota yang semuanya harus dikunjungi tepat satu kali.
3. Perjalanan tidak boleh kembali ke kota awal (depot) sebelum semua kota tujuan dikunjungi.
4. Tujuan dari permasalahan ini adalah meminimalkan total jarak yang ditempuh salesman dengan mengatur urutan kota yang harus dikunjungi.  

Tahapan – Tahapan Algoritma Genetika (Genetic Algorithm)

Berikut ini tahapan – tahapan (diagram alir) algoritma genetika:

1. Inisialisasi

Pada tahap ini menentukan jumlah gen dalam satu kromosom, yaitu sebanyak kota. Tentukan ukuran populasi, tentukan probabilitas crossover, tentukan probabilitas mutasi.

2. Bangkitkan populasi awal

Pada tahap ini yaitu membangkitkan sejumlah rute sebanyak ukuran populasi secara random.

3. Lakukan penghitungan nilai fitness

Penghitungan nilai fitness dilakukan dengan menghitung jarak total dari rute yang dihasilkan. Pilih individu terbaik, yang dilihat dengan memilih rute terpendek.

4. Salin individu terbaik

Pada tahap ini yaitu menyalin individu terbaik untuk disimpan dalam populasi berikutnya tanpa mengalami kawin silang atau mutasi.

5. Seleksi Parents

Pada tahap ini yaitu memilih induk / orang tua yang nantinya akan melakukan proses kawin silang (crossover).

6. Crossover

Tahap dimana proses kawin silang terjadi.

7. Mutasi

Lakukan proses mutasi dengan menukarkan urutan kota dalam satu individu. Langkah ini adalah langkah untuk memunculkan kemungkinan solusi baru. Namun diusahakan tidak terlalu banyak individu yang mengalami mutasi, dengan menerapkan nilai peluang mutasi yang cukup kecil. Proses dari tahap 3 (menghitung nilai fitness) sampai tahap 7 (mutasi) akan dilakukan terus menerus dan akan berhenti apabila iterasi maksimum terpenuhi. 

Berikut ini gambar tahapan diagram alir algoritma genetika:  

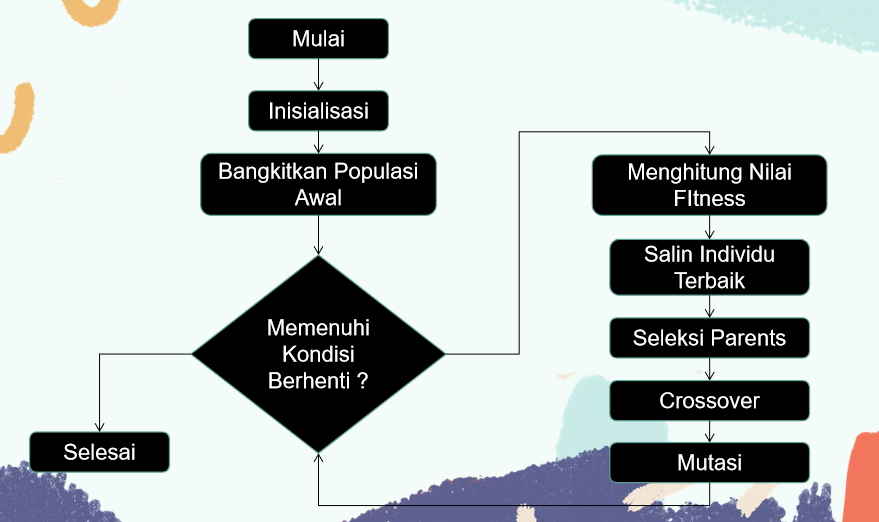Tahapan - Tahapan Algoritma Genetika

Coding Algoritma Genetika untuk Kasus TSP Menggunakan Matlab

Berikut ini coding / source code algoritma genetika untuk kasus TSP yang diimplementasikan menggunakan software Matlab:

function [RuteTerbaik,jarak]=tspga(xy,N,Maxit)

%Input:

% xy= [2 3; 1 7; 3 9; 5 3; 7 2; 9 5; 9 10; 11 1; 15 7; 19 2];

% xy= [0 132 217 164 58;

%     132 0 290 201 79;

%     217 290 0 113 303;

%     164 201 113 0 196;

%     58 79 303 196 0]

 

% N= Jumlah kromosom dalam populasi

% Maxit= Jumlah iterasi maksimum

t= cputime; %awal waktu komputasi 

 

jgen= length(xy); % Jumlah Gen (jumlah kota)

Psilang= 0.8; % Probabilitas Pindah silang

Pmutasi= 0.01; % Probabilitas mutasi

Fthreshold= 0.0001;% Threshold untuk fitness

 

%% menghitung matrik jarak antar kota

for i=1:jgen

    for j=1:jgen

        cost(i,j)=sqrt((xy(i,1)-xy(j,1))^2+(xy(i,2)-xy(j,2))^2);

    end

end

dx=cost;

 

%% Inisialisasi populasi

Populasi= tspinisialisasi(N,jgen);

d=size(xy);

if d(2)>2

    dx=xy;

end

 

for generasi=1:Maxit

    for i=1:N

        Fitness(i)=1/jartsp(Populasi(i,:),dx);

    end

    [MaxF,idk]= max(Fitness);

    RuteTerbaik= Populasi(idk,:);

    MinF= min(Fitness);

    if MinF < Fthreshold

        break;

    end

    Populasi_s= Populasi;

    % Elitisme:

    % Buat 4 kopi dari kromosom terbaik jika ukuran populasi genap

    % Buat 3 kopi dari kromosom terbaik jika ukuran populasi ganjil

    if mod(N,2)==0; % ukuran populasi genap

        IterasiMulai= 5;

        Populasi_s(1,:)= Populasi(idk,:);

        Populasi_s(2,:)= Populasi(idk,:);

        Populasi_s(3,:)= Populasi(idk,:);

        Populasi_s(4,:)= Populasi(idk,:);

    else % ukuran populasi ganji

        IterasiMulai= 4;

        Populasi_s(1,:)= Populasi(idk,:);

        Populasi_s(2,:)= Populasi(idk,:);

        Populasi_s(3,:)= Populasi(idk,:);

    end

   

    %% Roulette-Wheel selection dan pindah silang 

    for j= IterasiMulai:2:N 

       [Bapak,Ibu]= lotere(N,Fitness,jgen);

       r= rand;

        if r < Psilang

           for i= 1:N

               P1=Populasi(i,:);

               P1(P1==1)=[];

               Pop1(i,:)=P1; %Populasi tanpa kota 1

           end

           %% crossover  

            Anak= TSPPindahSilang(Pop1(Bapak,:),Pop1(Ibu,:),jgen);

            anak1=[1 Anak(1,:) 1];

            anak2=[1 Anak(2,:) 1];

            Populasi_s(j,:)= anak1;

            Populasi_s(j+1,:)= anak2;

        else

            Populasi_s(j,:)= Populasi(Bapak,:);

            Populasi_s(j+1,:)= Populasi(Ibu,:);

        end

    end

    %% Mutasi dilakukan pada seperempat kromosom

    for kk= IterasiMulai:(0.25*N)

            for i= 1:N

               P1=Populasi_s(i,:);

               P1(P1==1)=[];

               Pop1(i,:)=P1; %Populasi tanpa kota 1

           end

        Mutcrom= TSPMutasi(Pop1(kk,:),jgen,Pmutasi);

        Populasi_s(kk,:)= [1 Mutcrom 1];

    end

    Populasi= Populasi_s;

end

jater= RuteTerbaik;

jarak= jartsp(jater,dx);

t=cputime-t % total waktu komputasi (detik)

 

%%%%%%%%%%%%%%%%%%% inisialisasi populasi 

function Populasi= tspinisialisasi(N,jgen)

for i=1:N

    Pop(i,:)= randperm(jgen);

    pop= Pop(i,:);

    pop(pop==1)=[];

    Populasi(i,:)= [1 pop 1];

end

%% menghitung jarak

function jarak=jartsp(x1,dx)

[r,c]=size(x1); 

k=c-1; %jumlah kota dalam rute tsp 

s=0; %jarak awal di kota pertama 

for j=1:k 

    s=s+dx(x1(j),x1(j+1)); %pengakumulasian jarak rute tsp 

end

jarak=s;

 

%% selection 

function [Bapak,Ibu]= lotere(N,Fitness,jgen)   

    rtf=zeros(1,N);

    pnt=zeros(1,2);

    for i=1:N

        rtf(i)=Fitness(i);

    end

    rtf=rtf/sum(rtf);

    rtf=cumsum(rtf);

    while pnt(1)==pnt(2)

        rn1=rand(); rn2=rand();

        pnt(1)=find(rtf>rn1,1,'first');

        pnt(2)=find(rtf>rn2,1,'first');

        Bapak= pnt(1);

        Ibu= pnt(2);

    end

    

   %% mutasi kromosom  

function MutKrom= TSPMutasi(Kromosom,JumGen,Pmutasi)

MutKrom= Kromosom;

G=JumGen-1;

for i=1:G

    r= rand;

    if r < Pmutasi

        TM2= 1+fix(rand*G);

        while TM2==i

            TM2= 1+ fix(rand*G);

        end

        temp= MutKrom(i);

        MutKrom(i)= MutKrom(TM2);

        MutKrom(TM2)= temp;

    end   

end

 

%% crossover 

function Anak= TSPPindahSilang(Bapak,Ibu,JumGen)

% Dari lampiran buku Suyanto Algoritma Genetika dalam Matlab

% Andi offet 2005

cp1= 1+fix(rand*(JumGen-1));

cp2= 1+fix(rand*(JumGen-1));

while cp2==cp1

    cp2= 1+fix(rand*(JumGen-1));

end

if cp1 < cp2

    cps= cp1;

    cpd= cp2;

else

    cps= cp2;

    cpd= cp1;

end

Anak(1,cps+1:cpd)= Ibu(cps+1:cpd);

Anak(2,cps+1:cpd)= Bapak(cps+1:cpd);

SisaGenbapak= [];

SisaGenIbu= [];

 

G= JumGen-1 ;

for i= 1:G

    if ~ismember(Bapak(i),Anak(1,:));

        SisaGenbapak= [SisaGenbapak Bapak(i)];

    end

    if ~ismember(Ibu(i),Anak(2,:));

        SisaGenIbu= [SisaGenIbu Ibu(i)];

    end

end

Anak(1,cpd+1:G)= SisaGenbapak(1:G-cpd);

Anak(1,1:cps)= SisaGenbapak(1+G-cpd:length(SisaGenbapak));

Anak(2,cpd+1:G)= SisaGenIbu(1:G-cpd);

Anak(2,1:cps)= SisaGenIbu(1+G-cpd:length(SisaGenIbu)); 

Langkah-langkah Running Algoritma Genetika dengan Matlab

1. Buka software Matlab

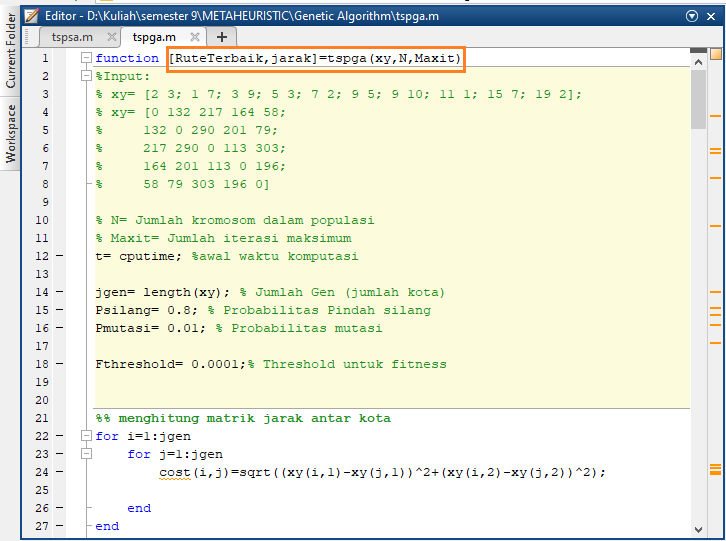
2. Buka file Algoritma Genetika yang akan dirunning, selanjutnya tekan tombol run

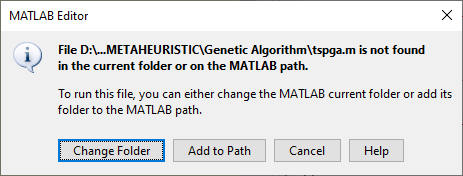
3. Setelah langkah tersebut, maka muncul kotak dialog MATLAB Editor, pilih Change Folder agar file algoritma genetika berada di Current Folder.

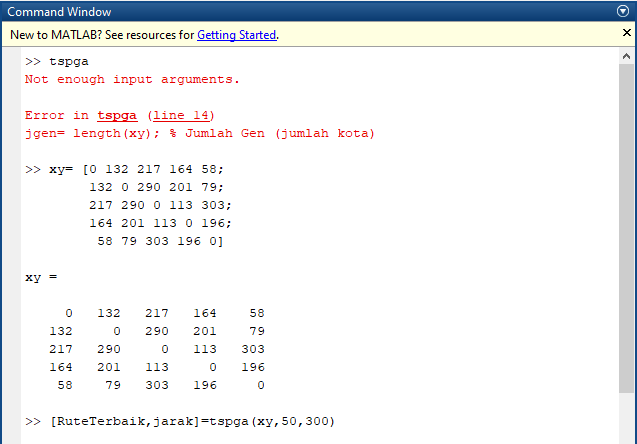
4. Masukkan matrik jarak permasalahan TSP pada area Command Window.

5. Selanjutnya copy function algoritma Genetika, lalu paste ke area Command Window.

6. Ubah N dan Maxit, sesuai keinginan. Pada contoh kali ini menggunakan N = 50 dan Maxit = 300. 

Catatan: Anda dapat mengubah N, Maxit, Probabilitas Crossover, dan Probablitas Mutasi sesuai keinginan.

7. Jika sudah, selanjutnya tekan enter, maka akan muncul output seperti berikut:

Output TSP dengan Algoritma Genetika

Output yang muncul yaitu t, Rute Terbaik, dan Jarak. Diperoleh waktu komputasi atau t selama 1,1875 detik. Rute terbaik diperoleh 1-3-4-2-5-1 dengan total jarak 668. 

Anda juga dapat melihat pembahasan artikel ini dalam bentuk penjelasan video berikut ini:

Demikian artikel dengan judul Travelling Salesman Problem Menggunakan Algoritma Genetika, semoga artikel ini bermanfaat. Terima kasih telah berkunjung di blog faqirilmu.com.

Referensi:

Santosa, Budi & Ai, Jin. 2017. Pengantar Metaheuristik Implementasi dengan Matlab. ITS Tekno Sains: Surabaya.