Cara Analisis Regresi Linear Berganda dengan SPSS

Analisis Regresi Linear Berganda dengan SPSS

Pengertian Analisis Regresi Linear Berganda

Analisis regresi linear berganda adalah analisis yang digunakan untuk mengetahui pengaruh dua atau lebih variabel independen terhadap variabel dependen. Selain itu analisis regresi linear berganda juga digunakan untuk meramalkan suatu variabel dependen berdasarkan beberapa variabel independen. Regresi linear berganda disebut juga dengan regresi berganda. Pada regresi linear, variabel independen disimbolkan dengan X dan variabel dependen disimbolkan dengan Y. 

Perbedaan regresi linear berganda dengan regresi linear sederhana 

Apakah Anda tahu perbedaan regresi linear berganda dengan regresi linear sederhana? Perbedaan regresi linear berganda dengan regresi linear sederhana terletak pada jumlah variabel independen. Apabila pada regresi linear sederhana hanya terdapat satu variabel independen, sedangkan pada regresi linear berganda terdapat dua atau lebih variabel independen yang mempengaruhi variabel dependen.

Persamaan Regresi Linear Berganda

Dibawah ini merupakan persamaan regresi berganda:

Y = a + b1X1 + b2X2

Keterangan dari persamaan diatas adalah sebagai berikut: 

Y                = variabel dependen atau variabel respon.
X1 dan X2 = variabel independen atau variabel faktor.
a                = konstanta persamaan regresi (nilai dari Y jika X1 dan X2 = 0).
b1 dan b2  = koefisien regresi (bisa berpengaruh positif atau negatif).

Uji Asumsi Klasik Regresi Linear Berganda 

Sebelum melakukan analisis regresi berganda, perlu melakukan uji prasyarat atau uji asumsi klasik. Uji asumsi klasik dilakukan agar diketahui apakah model regresi tersebut merupakan model regresi yang baik atau tidak. Berikut ini uji asumsi klasik untuk regresi berganda:

1. Uji normalitas residual

Uji normalitas untuk regresi linear digunakan untuk mengetahui apakah nilai residual yang dihasilkan dari regresi terdistribusi secara normal atau tidak. Model regresi dikatakan baik apabila memiliki nilai residual yang berdistribusi normal. 

Artikel terkait: Cara uji normalitas residual One Sample Kolmogorov-Smirnov

2. Uji heteroskedastisitas

Heteroskedastisitas menunjukkan bahwa varian variabel-variabel tidak sama untuk semua pengamatan. Model regresi yang baik apabila tidak terjadi heteroskedastisitas. 

Artikel terkait: Cara uji heteroskedastisitas dengan SPSS

3. Uji Multikolinearitas 

Uji multikolinearitas digunakan untuk mengetahui apakah antar variabel independen yang terdapat dalam model regresi linear mempunyai hubungan linear yang sempurna atau mendekati sempurna. (koefisien korelasinya tinggi atau bahkan 1). Model regresi yang baik seharusnya tidak terjadi multikolinearitas. 

Artikel terkait: Cara uji Multikolinearitas dengan SPSS

4. Uji Autokorelasi 

Autokorelasi adalah korelasi yang terjadi antara anggota-anggota dari serangkaian pengamatan yang tersusun dalam rangkaian waktu. Model regresi yang baik seharusnya tidak terjadi autokorelasi. Beberapa sumber menyatakan bahwa, untuk uji autokorelasi hanya dilakukan apabila data penelitian berupa time series atau data runtut waktu.

Contoh Kasus Analisis Regresi Berganda

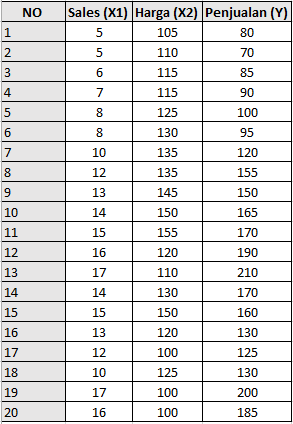
Seorang Manajer pemasaran suatu perusahaan ingin melakukan peramalan atas besarnya jumlah penjualan berdasarkan jumlah sales dan harga produk. Terdapat tiga variabel penelitian. Jumlah sales dan harga produk merupakan variabel independen dan penjualan merupakan variabel dependen. Berikut ini datanya:

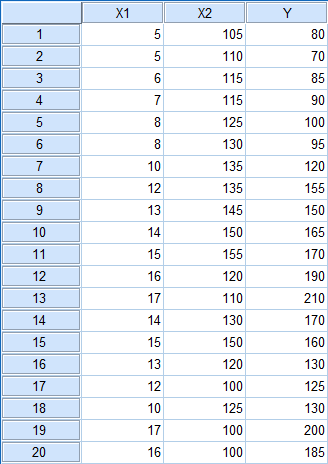Tampilan Data View SPSS

Tampilan Variable View SPSS

Data diatas sudah dimasukkan pada software SPSS, selanjutnya melakukan analisis regresi linear berganda. Sebelum melakukan uji regresi linear berganda, terlebih dahulu perlu melakukan uji asumsi klasik. Pada artikel ini hanya akan membahas analisis regresi berganda.

Langkah-Langkah Uji Regresi Linear Berganda dengan SPSS

Berikut ini langkah-langkah uji regresi berganda menggunakan IBM SPSS:

1. Setelah melakukan input data di SPSS. Selanjutnya melakukan analisis regresi linear berganda dengan klik Analyze, pilih Regression, lalu pilih Linear pada menu, sehingga muncul kotak dialog Linear Regression.

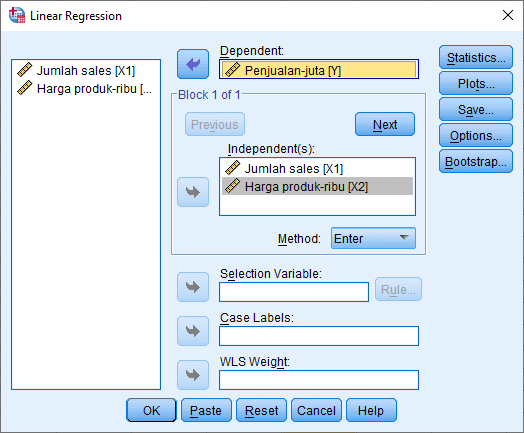
2. Masukkan variabel jumlah sales (X1) dan harga (X2) pada kotak Independent(s) dan variabel penjualan (Y) ke kotak Dependent.

3. Selanjutnya klik tab Statistics, sehingga akan muncul kotak dialog Linear Regression: Statistics. Beri centang pada Estimates dan Model fit. 

4. Kemudian klik Continue, sehingga kembali ke kotak dialog awal, lalu klik OK, sehingga SPSS menampilkan hasil sebagai berikut:

Interpretasi Hasil Uji Regresi Berganda dengan SPSS

Ada empat output atau tabel hasil analisis regresi linear berganda, berikut ini cara membaca hasil regresi linear berganda:

Output pertama Variables Entered/Removed

Output tabel Variables Entered/Removed menginformasikan metode regresi linear yang dipilih, yaitu metode enter. Dari output dapat dilihat bahwa variabel independen yang dimasukkan ke dalam model adalah variabel jumlah sales dan harga, untuk variabel dependennya adalah variabel penjualan. Tidak ada variabel yang dikeluarkan (removed).

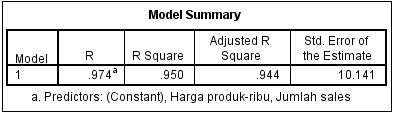
Output kedua Model Summary 

Tabel Model Summary menginformasikan besarnya nilai korelasi (R), koefisien determinasi (R2), Adjusted R Squre, dan Std. Error of the Estimate.

R adalah korelasi berganda, yaitu korelasi antara dua atau lebih variabel independen terhadap variabel dependen. Nilai R berkisar antara 0 sampai 1, jika mendekati 1 maka hubungan semakin erat, tetapi apabila mendekati 0 maka hubungan semakin lemah. Nilai R diperoleh 0,974 yang mampunyai arti korelasi antara variabel jumlah sales dan harga terhadap variabel penjualan sebesar 0,974. 

R square atau kuadrat dari R, menunjukkan koefisien determinasi. Angka ini akan diubah ke bentuk persen, yang berarti besar pengaruh variabel independen terhadap variabel dependen. Diperoleh nilai koefisien determinasi 0,950, yang berarti besar pengaruh variabel jumlah sales dan harga terhadap variabel penjualan sebesar 95,0% sedangkan sisanya 5% dipengaruhi oleh variabel lain yang tidak dimasukkan dalam model ini.

Adjusted R Square merupakan R Square yang telah disesuaikan, dengan nilai 0,944. Adjusted R Square biasanya digunakan untuk mengukur sumbangan pengaruh jika dalam model regresi menggunakan lebih dari dua variabel independen. 

Std Error of the Estimate, adalah ukuran kesalahan prediksi dengan nilai 10,141. Angka tersebut mempunyai arti kesalahan yang dapat terjadi dalam memprediksi variabel penjualan sebesar 10,141.

Output ketiga ANOVA

ANOVA atau analisis varian, yaitu uji koefisien regresi secara bersama-sama untuk menguji signifikansi pengaruh beberapa variabel independen terhadap variabel dependen. 

Output ANOVA atau disebut uji F, merupakan tabel yang akan digunakan untuk menjawab hipotesis regresi linear berganda. 

Berikut ini rumusan hipotesis regresi linear berganda untuk permasalahan diatas:

H0 = Variabel X1 (jumlah sales) dan X2 (harga) secara bersama-sama tidak berpengaruh terhadap variabel Y (penjualan).
H1 = Variabel X1 (jumlah sales) dan X2 (harga) secara bersama-sama berpengaruh terhadap variabel Y (penjualan).

Setelah mengetahui hipotesisnya, Anda harus tahu pedoman pengambilan keputusan. Berikut ini pedoman pengambilan keputusan uji regresi berganda:

Apabila nilai signifikansi (Sig.) > 0,05 maka H0 diterima 
Apabila nilai signifikansi (Sig.) < 0,05 maka H0 ditolak

Pada tabel ANOVA diperoleh nilai Sig. (0,000) < 0,05 maka Ho ditolak. Karena H0 ditolak maka H1 diterima, jadi Variabel X1 (jumlah sales) dan X2 (harga) secara bersama-sama berpengaruh terhadap variabel Y (penjualan).

Output keempat Coefficients

Tabel Coefficient menginformasikan besarnya nilai B, Std. Error, Beta, Nilai t dan nilai Sig. Berikut ini penjelasan dari masing-masing nilai tersebut:

Unstandardized Coefficient, adalah nilai koefisien yang tidak terstandarisasi atau tidak ada patokan. Nilai ini menggunakan satuan yang digunakan pada data dari variabel dependen. Kolom B terdiri nilai konstan (nilai Y jika X1 dan X2 = 0) dan koefisien regresi (nilai yang menunjukkan peningkatan atau penurunan variabel Y yang disebabkan variabel X1 dan X2), nilai-nilai inilah yang masuk dalam persamaan regresi linear berganda. 

Std. Error adalah nilai maksimum kesalahan yang dapat terjadi dalam memperkirakan rata-rata populasi berdasarkan sampel. Nilai ini untuk mencari nilai t hitung dengan cara koefisien dibagi standard error. 

Standardized Coefficients, merupakan nilai koefisien yang telah terstandarisasi atau ada patokan tertentu. Nilai koefisien Beta semakin mendekati 0, maka hubungan antara variabel X dengan Y semakin lemah. 

t hitung adalah pengujian signifikansi untuk mengetahui pengaruh variabel X1 dan X2 terhadap variabel Y secara parsial, apakah berpengaruh signifikan atau tidak. Untuk mengetahui apakah hasil signifikan atau tidak, nilai t hitung akan dibandingkan dengan nilai t tabel.

Signifikansi atau Sig adalah besarnya probabilitas atau peluang untuk memperoleh kesalahan dalam mengambil keputusan. Jika pengujian menggunakan tingkat signifikansi 0,05 artinya peluang memperoleh kesalahan maksimal 5%, dengan kata lain kita percaya bahwa 95% keputusan adalah benar. 

Persamaan Regresi Linear Berganda

Untuk melihat model persamaan regresi, kita fokus ke kolom B. Pada kolom B diperoleh nilai Constant (a) sebesar 28,054 sedangkan nilai koefisien regresi variabel X1 (jumlah sales) sebesar 10,412 dan variabel X2 (harga) sebesar -0,084. Persamaan regresi berganda dapat ditulis:

Y = a + b1X1 + b2X2  (rumus dasar)

Y = 28,054 + 10,412 X1 -0,084 X2

Atau bisa juga ditulis seperti berikut

Penjualan = 28,054 + 10,412 jumlah sales -0,084 harga

Persamaan regresi tersebut dapat diterjemahkan sebagai berikut:

• Konstanta a sebesar 28,054, angka ini merupakan angka konstan yang mempunyai arti jika variabel jumlah sales (X1) dan harga (X2) nilainya 0 maka variabel penjualan Y bernilai 28,054.
• Nilai koefisien regresi variabel jumlah sales (X1) bernilai positif yaitu sebesar 10,412. Angka ini mengandung arti bahwa setiap penambahan nilai sebesar 1 satuan pada variabel jumlah sales (X1), maka nilai variabel penjualan akan meningkat sebesar 10,412 satuan dengan asumsi variabel independen lainnya nilainya tetap. 
• Nilai koefisien regresi variabel harga (X2) bernilai negatif yaitu sebesar -0,084. Angka ini mengandung arti bahwa setiap penambahan nilai sebesar 1 satuan pada variabel harga (X2), maka nilai variabel penjualan akan menurun sebesar 0,084 satuan dengan asumsi variabel independen lainnya nilainya tetap. 

Uji t 

Uji t (uji koefisien regresi secara parsial) digunakan untuk mengetahui apakah secara parsial variabel jumlah sales dan harga berpengaruh secara signifikan atau tidak terhadap variabel penjualan. 

Pengujian koefisien variabel jumlah sales (b1)

Rumusan hipotesis

H0 = jumlah sales secara parsial tidak berpengaruh terhadap penjualan.
H1 = jumlah sales secara parsial berpengaruh terhadap penjualan.

Pedoman pengambilan keputusan

Jika nilai Sig > 0,05 maka H0 diterima
Jika nilai Sig < 0,05 maka H0 ditolak

Pada tabel Coefficients di baris jumlah sales diperolah nilai Sig sebesar 0,000 < 0,05 maka H0 ditolak. Karena H0 ditolak maka H1 diterima, jadi jumlah sales secara parsial berpengaruh terhadap penjualan.

Pengujian koefisien variabel harga (b2)

Rumusan hipotesis

H0 = harga secara parsial tidak berpengaruh terhadap penjualan.
H1 = harga secara parsial berpengaruh terhadap penjualan.

Pedoman pengambilan keputusan

Jika nilai Sig > 0,05 maka H0 diterima
Jika nilai Sig < 0,05 maka H0 ditolak

Pada tabel Coefficients di baris variabel harga diperolah nilai Sig 0,546 > 0,05 maka H0 diterima, jadi harga secara parsial tidak berpengaruh terhadap penjualan.

Anda juga dapat melihat pembahasan Analisis Regresi Linear Berganda dengan SPSS dalam bentuk penjelasan video berikut ini:

OK demikian artikel tentang Cara Analisis Regresi Linear Berganda dengan SPSS. Semoga artikel ini mudah dipahami ya. Terima kasih sudah berkunjung di blog faqirilmu.com.

Referensi: 

Trihendradi, C., 2013. Step by Step IBM SPSS 21: Analisis Data Statistik. Yogyakarta: Penerbit Andi.
Purnomo, R. A. 2016. Analisis Statistik Ekonomi dan Bisnis dengan SPSS. Ponorogo: Penerbit Wade Group.