Cara Uji Two Way ANOVA Menggunakan SPSS

Pengertian Two Way ANOVA

Two Way ANOVA adalah uji yang digunakan untuk mengetahui adanya pengaruh variabel 1 maupun variabel 2 terhadap suatu populasi serta mengetahui interaksi dari kedua variabel faktor. Uji Two way ANOVA disebut juga dengan uji anova dua  faktor. 

Pada Anova dua faktor berarti terdapat dua faktor yang berpengaruh pada suatu populasi tertentu. Kedua faktor tersebut menyebabkan efek utama yang dapat berpengaruh positif atau negatif, sehingga perlu melakukan uji keberartian antar faktor apakah terdapat interaksi antar faktor atau tidak.

Perbedaan Uji One Way ANOVA dengan Two Way ANOVA

Pada artikel sebelumnya kita telah mempelajari analisis one way ANOVA. Pada one way ANOVA hanya terdapat satu faktor atau satu variabel bebas terhadap variabel respon. 

Pada two way ANOVA terdapat dua faktor atau dua variabel bebas terhadap variabel respon. Karena terdapat dua variabel faktor, maka pada uji two way ANOVA dapat melihat apakah antar kedua faktor tersebut ada interaksi atau tidak.

Syarat Uji Two Way ANOVA

Setiap data yang terkumpul pasti memiliki karakteristik tersendiri, sehingga dibutuhkan metode uji statistik yang tepat. Begitu juga untuk uji Two Way ANOVA. Berikut ini persyaratan penggunaan uji Two Way ANOVA:

  1. Terdapat 2 faktor (variabel independen) yang berupa data kategorikal.
  2. Variabel dependen berupa data metrik (bisa data interval/rasio).
  3. Residual data penelitian berdistribusi normal.  
  4. Variabel data penelitian Homogen.

Terkait penjelasan lengkap mengenai uji homogenitas bisa lihat pada link berikut ini:
Uji Homogenitas dengan SPSS

Contoh Kasus Uji Two Way ANOVA

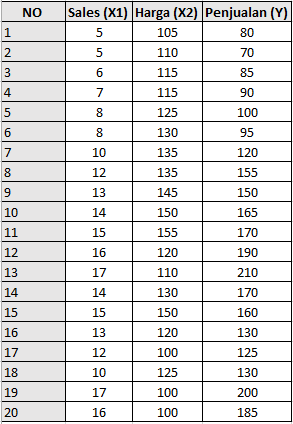
Seorang peneliti ingin mengetahui apakah karakteristik kemasan dan harga mempengaruhi tingkat penjualan. Dari data tersebut Anda diminta untuk membuktikan apakah ada pengaruh atau efek dari karakteristik besarnya kemasan dan harga terhadap tingkat penjualan, serta interaksi dari keduanya dalam memengaruhi tingkat penjualan. Berikut ini data tingkat penjualan:

Data Tingkat Penjualan

Cara Uji Two Way ANOVA dengan SPSS

Berikut ini langkah-langkah uji two way ANOVA dengan SPSS:

1. Buka software SPSS, langkah awal yaitu input data di SPSS dengan cara klik Variable View untuk membuat variabel. Pada kolom Name ketik Harga pada baris pertama, Kemasan pada baris kedua, dan Penjualan pada baris ketiga.

Pada kolom Label ketik Tingkat Harga pada baris pertama, Karakteristik Kemasan pada baris kedua, dan Tingkat Penjualan pada baris ketiga.

Pada kolom Decimals, kita tetapkan jumlah digit setelah koma. Untuk variabel Harga = 0, variabel Kemasan = 0, dan variabel Penjualan = 1(karena data terdapat satu angka dibelakang koma).

Pada kolom Values untuk variabel Harga kita beri kode, 1 untuk Harga tinggi dan 2 untuk harga rendah. Untuk variabel Kemasan kita beri kode, 1 untuk kecil, 2 untuk sedang, dan 3 untuk besar.

Kolom Values SPSS

Untuk kolom-kolom lainnya tidak perlu di setting (tidak perlu di ubah-ubah). Berikut ini tampilan variable view SPSS

Tampilan Variable View SPSS

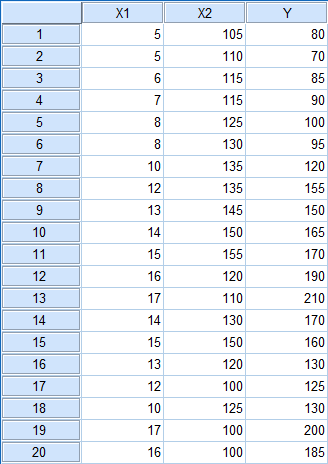
2. Selanjutnya kita input data dengan cara klik bagian Data View, lalu menuliskan langsung data pada SPSS. Apabila data Anda sudah disusun di Microsoft Excel maka bisa dengan cara copy dan paste. Berikut ini tampilan Data View SPSS

Tampilan Data View SPSS
Tampilan Data View SPSS (sebagian data)

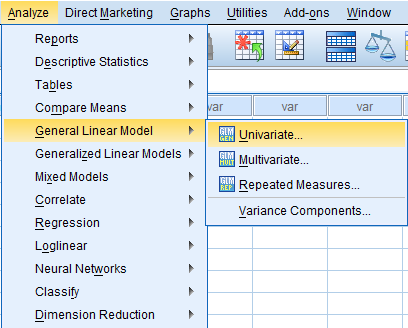
3. Setelah selesai input data, lanjut analisis Two Way ANOVA dengan cara klik Analyze, pilih General Linear Model, lalu pilih Univariate.

Langkah-langkah uji two way ANOVA

4. Setelah langkah tersebut maka akan keluar kotak dialog Univariate. Masukkan Variabel Harga dan Variabel Kemasan pada kotak Fixed Factor, variabel Penjualan pada kotak Dependent Variable.

Kotak dialog univariate

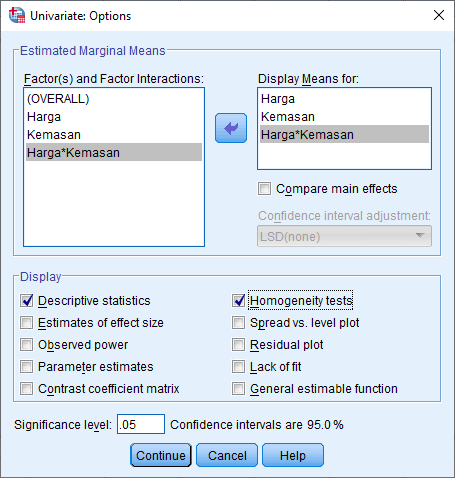
5. Selanjutnya klik Options, maka akan muncul kotak dialog Univariate: Options. Masukkan variabel Harga, Kemasan, dan Harga*Kemasan ke kotak Display Means for. Kemudian pada kotak Display beri centang Homogeneity tests dan Descriptive statistics.

Kotak dialog univariate: options

6. Selanjutnya klik Continue, lalu klik OK, sehingga output SPSS menampilkan hasil sebagai berikut.

Interpretasi Output Uji Two Way ANOVA

Output Levene’s Test of Equality of Error Variances

Output Tabel Levene’s Test of Equality of Error Variances digunakan untuk melihat apakah varian variabel dependent adalah homogen atau tidak. Adapun pedoman pengambilan keputusan untuk uji homogenitas adalah sebagai berikut:

  • Jika nilai Sig. > ɑ (0.05) maka varian variabel tingkat penjualan adalah sama (homogen)
  • Jika nilai Sig. < ɑ (0.05) maka varian variabel tingkat penjualan adalah tidak sama (tidak homogen)

Berdasarkan output diatas diperoleh nilai Sig (0.605) >  ɑ (0.05) maka varian variabel tingkat penjualan adalah sama (homogen). Karena varian variabel tingkat penjualan homogen, maka data ini telah memenuhi persyaratan uji two way anova.

Output Between Subjects Factors

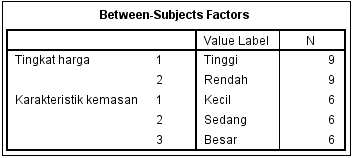
Output Tabel Between Subjects Factors menampilkan hasil dari subjek-subjek yang kita teliti. Subjek-subjek yang diteliti dimasukkan dalam analisis data sesuai dengan faktor yang berbeda antar masing-masing variabel. 

Output Descriptive Statistics SPSS

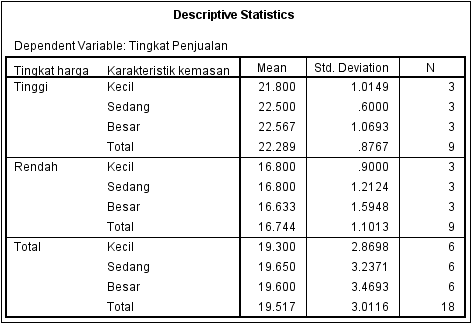
Output Tabel Descriptive Statistics menampilkan statistik deskriptif dari data yang dianalisis. Pada tabel tersebut menampilkan nilai mean, standar deviasi dan N (jumlah masing-masing data).

Output Tests of Between-Subjects Effects

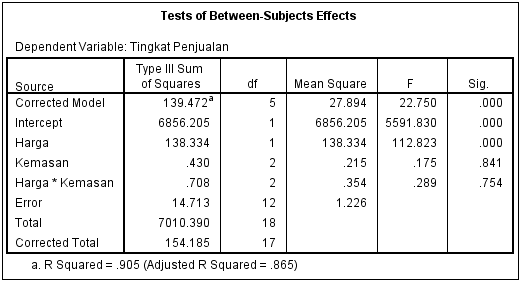
Output tabel Tests of Between-Subjects Effects merupakan tabel yang digunakan untuk menjawab hipotesis penelitian ini. Kolom yang digunakan untuk menguji hipotesis yaitu pada kolom Sig. (signifikansi). Ada tiga hipotesis untuk uji Two Way ANOVA, berikut ini hipotesisnya

Hipotesis Uji Two Way ANOVA

Hipotesis Variabel Harga

H0 = tidak ada perbedaan tingkat penjualan berdasarkan tingkat harga
H1 = ada perbedaan tingkat penjualan berdasarkan tingkat harga

Hipotesis Variabel Kemasan

H0 = tidak ada perbedaan tingkat penjualan berdasarkan karakteristik kemasan
H1 = ada perbedaan tingkat penjualan berdasarkan karakteristk kemasan

Hipotesis Interaksi Variabel Harga dan Kemasan

H0 = tidak ada interaksi tingkat harga dan karakteristik kemasan dalam mempengaruhi tingkat penjualan.
H1 = ada interaksi tingkat harga dan karakteristik kemasan dalam mempengaruhi tingkat penjualan.

Pedoman Pengambilan Keputusan Uji Two Way ANOVA

Untuk menjawab hipotesis diatas, maka diperlukan pedoman/aturan dalam mengambil keputusan. Berikut ini pedoman Pengambilan Keputusan Uji Two Way ANOVA:

  • Jika nilai Sig (signifikansi) > ɑ (0.05) maka H0 diterima
  • Jika nilai Sig (signifikansi) < ɑ (0.05) maka H0 ditolak

Membaca Tabel Tests of Between-Subjects Effects 

Hipotesis Variabel Harga
Diperoleh nilai Sig  (0.000) < (0.05) maka H0 ditolak, maka ada perbedaan tingkat penjualan berdasarkan tingkat harga

Hipotesis Variabel Kemasan
Diperoleh nilai Sig  (0.841) > (0.05) maka H0 diterima, maka tidak ada perbedaan tingkat penjualan berdasarkan karakteristik kemasan

Hipotesis Interaksi Variabel Harga dan Kemasan
Diperoleh nilai Sig  (0.754) > (0.05) maka H0 diterima, maka tidak ada interaksi tingkat harga dan karakteristik kemasan dalam mempengaruhi tingkat penjualan.

Output Estimated Marginal Means

Output Estimated Marginal Means Tingkat Harga
Output Estimated Marginal Means Karakteristik Kemasan
Output Estimated Marginal Means Tingkat Harga * Karakteristik Kemasan

Output Estimated Marginal Means menampilkan perbedaan nilai rata-rata tingkat penjualan berdasarkan variabel tingkat harga, variabel karakteristik kemasan dan interaksi tingkat harga dengan karakteristik kemasan.

Kesimpulan Uji Two Way ANOVA 

Berdasarkan uji two way anova yang telah Kita lakukan untuk contoh kasus diatas, maka dapat disimpulkan:

1.Terdapat perbedaan tingkat penjualan berdasarkan tingkat harga. Dengan kata lain, tingkat harga yang berbeda memberikan pengaruh terhadap tingkat penjualan.

2.Tidak terdapat perbedaan tingkat penjualan berdasarkan karakteristik kemasan. Dengan kata lain, karakteristik kemasan yang berbeda tidak memberikan pengaruh yang nyata terhadap tingkat penjualan.

3.Tidak terdapat interaksi antara tingkat harga dan karakteristik kemasan dalam mempengaruhi tingkat penjualan. 

Anda juga dapat melihat tutorial Cara Uji Two Way ANOVA dengan SPSS dalam bentuk penjelasan video berikut ini.



Demikian artikel terkait Cara Uji Two Way ANOVA dengan SPSS, semoga artikel ini bermanfaat. Terimakasih telah mengunjungi blog faqirilmu.com


Referensi:

https://www.statistikian.com/2012/11/two-way-anova-dalam-spss.html
https://www.spssindonesia.com/2018/03/uji-two-way-anova-spss.html










Komentar

Posting Komentar

Postingan populer dari blog ini

Perbedaan Scale, Nominal dan Ordinal pada Measure di SPSS

Gambar
Perbedaan Scale, Nominal dan Ordinal pada Measure di SPSS      Measure merupakan salah satu kolom yang berada di variable view IBM SPSS. Kolom measure harus ditetapkan terlebih dahulu sebelum melakukan analisis data lebih lanjut. Terdapat 3 tipe variabel pada kolom measure SPSS yaitu scale, nominal dan ordinal . Ketiga variabel tersebut memberikan jenis nilai serta informasi analisis yang berbeda. Berikut ini pengertian dan perbedaan scale, nominal dan ordinal pada SPSS.      Penentuan measure merupakan hal dasar yang sangat penting untuk diketahui saat bekerja menggunakan SPSS. Misalnya kita tidak boleh membuat variabel nominal untuk melakukan perhitungan nilai rata-rata dan standar deviasi.  Pilihan untuk mengubah tipe variabel suatu variabel terdapat pada lembar kerja Variabel View SPSS. Gambar dibawah ini merupakan ilustrasinya. A.  Variabel Nominal pada SPSS      Variabel nominal merupakan tipe variabel yang digunakan hanya se...
Read more »

Cara Membaca nilai R Tabel dan Download R Tabel (Tabel R)

Gambar
Pengertian R Tabel Apa yang dimaksud R Tabel? R tabel merupakan sebuah tabel angka yang biasa dipakai untuk melakukan uji validitas suatu instrumen penelitian.  Fungsi R Tabel Berdasarkan definisi di atas, maka dapat diambil kesimpulan bahwa r tabel ini mempunyai fungsi untuk melakukan suatu pengujian terhadap instrumen penelitian agar mengetahui apakah instumen penelitian tersebut valid atau tidak.  Dibawah ini merupakan R tabel. Gambar Tabel R ( R Tabel) Mau mendownload R tabel? Silahkan melalui link dibawah ini.  DOWNLOAD R Tabel Cara Membaca Nilai r Tabel dalam Uji Validitas Pearson Ada beberapa cara dalam mengambil keputusan uji validitas. Cara yang pertama dengan menggunakan r tabel dan cara kedua dengan menggunakan nilai signifikansi . Berikut ini pedoman pengambilan keputusan uji validitas SPSS: Membandingkan Nilai r Hitung dengan Nilai r Tabel Jika nilai r hitung > r tabel, maka item pertanyaan kuesioner valid Jika nilai r hitung < r tabel, maka item perta...
Read more »

Cara Analisis Regresi Linear Berganda dengan SPSS

Gambar
Analisis Regresi Linear Berganda dengan SPSS Pengertian Analisis Regresi Linear Berganda Analisis regresi linear berganda adalah analisis yang digunakan untuk mengetahui pengaruh dua atau lebih variabel independen terhadap variabel dependen . Selain itu analisis regresi linear berganda juga digunakan untuk meramalkan suatu variabel dependen berdasarkan beberapa variabel independen. Regresi linear berganda disebut juga dengan regresi berganda . Pada regresi linear, variabel independen disimbolkan dengan X dan variabel dependen disimbolkan dengan Y.  Perbedaan regresi linear berganda dengan regresi linear sederhana  Apakah Anda tahu perbedaan regresi linear berganda dengan regresi linear sederhana ?  Perbedaan regresi linear berganda dengan regresi linear sederhana terletak pada jumlah variabel independen. Apabila pada regresi linear sederhana hanya terdapat satu variabel independen , sedangkan pada regresi linear berganda terdapat dua atau lebih variabel independen yan...
Read more »

Pengertian Uji T dan Uji F serta Cara Analisis dengan SPSS

Gambar
Pengertian Uji T dan Uji F pada Regresi Linear Berganda serta Cara Analisis dengan SPSS Pada artikel ini kita akan mempelajari cara uji t dan uji f pada regresi linear berganda dengan SPSS, serta cara interpretasi output uji t dan uji f. Kita mulai dari pengertian uji t Pengertian Uji T Uji t adalah uji yang digunakan untuk mengetahui ada tidaknya pengaruh secara parsial variabel independent (variabel X) terhadap variabel dependent (variabel Y). Maksud pengaruh parsial yaitu pengaruh sendiri-sendiri oleh variabel independent. Pada kasus uji regresi linear berganda dengan dua variabel independent, berarti kita akan melihat pengaruh variabel independent pertama (X1) terhadap variabel dependent (Y) dan melihat pengaruh variabel independent kedua (X2) terhadap variabel dependent (Y). Pada paragraf sebelumnya Saya menyebutkan regresi linear berganda. Apa itu uji regresi linear berganda ? Uji regresi linear berganda merupakan uji yang digunakan untuk mengetahui ada tidaknya pengaruh dari du...
Read more »

Analisis Crosstab dengan SPSS [Uji Chi-Square dan Correlation]

Gambar
Cara Analisis Crosstab Menggunakan SPSS  Pada artikel ini, Kita akan belajar analisis crosstabs menggunakan SPSS. Silahkan baca artikel ini sampai selesai ya, agar paham apa itu analisis crosstabs. Pada SPSS, analisis crosstab merupakan bagian dari statistik deskriptif . Lalu apa kegunaan analisis crosstabs? Analisis crosstab merupakan alat analisis untuk mendeskripsikan data dalam bentuk kolom dan baris. Selain itu digunakan untuk memeriksa hubungan antar variabel kategori (nominal atau ordinal). Analisis crosstab ini dibagi menjadi 2 bagian: Analisis Crosstab – Chi Square Analisis Crosstab – Correlations Lalu apa perbedaannya? Ok, kita langsung ke yang pertama, analisis Crosstab – Chi Square A. Analisis Crosstab Chi-Square Analisis Crosstab Chi-Square ini merupakan teknik analisis untuk melihat hubungan antar variabel data nominal. Syarat uji chi-squre ini variabel yang akan kita uji harus data nominal. Langsung aja ke contoh kasus, Suatu perusahaan mengamati apakah pelayanan k...
Read more »